| 문제 번호 |
| 문제 및 입/출력 |
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V(1≤V≤20,000)와 간선의 개수 E(1≤E≤200,000)가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호가 빈 칸을 사이에 두고 주어진다.
출력
K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.
| 예제 입력1 |
| 2 3 2 1 3 2 3 4 4 1 2 2 3 3 4 4 2 |
| 예제 출력1 |
| YES NO |
| 예제 입력2(반례 케이스, 출처: https://withallmy.tistory.com/113, 백준 질문게시판) |
| 11 3 1 2 3 3 2 1 3 2 3 4 4 1 2 2 3 3 4 4 2 3 2 2 1 3 2 4 4 2 1 3 2 4 3 4 1 5 2 1 5 1 2 5 2 1 2 2 5 4 3 1 2 4 3 2 3 4 4 2 3 1 4 3 4 1 2 3 3 1 2 2 3 3 1 2 1 1 2 |
| 예제 출력1 |
| YES YES NO YES YES YES YES YES YES NO YES |
| 문제 풀이 |
우선 이 문제를 풀기전에 이분 그래프(Bipartite Graph)라는것이 정확히 어떤 의미인지를 조사했다.
위키피아에서 나오는 이분 그래프의 정의는 다음과 같다.
그래프 이론에서, 이분 그래프(bipartite graph)란 모든 꼭짓점을 빨강(색1)과 파랑(색2)으로 색칠하되, 모든 변이 빨강(색1)과 파랑(색2) 꼭짓점을 포함하도록 색칠할 수 있는 그래프이다.
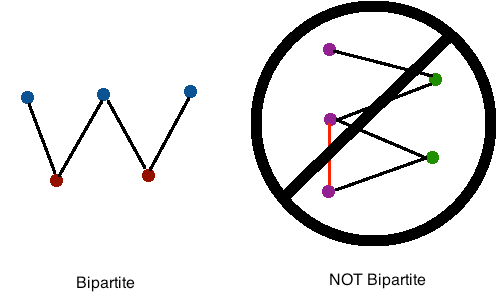
위 그림을 보면 확실히 구분이 가능한데,
- 왼쪽 그림을 보면 4개의 변으로 구성된 그래프로써, 각각의 변이 색1(파랑)과 색2(빨강)의 노드를 포함하는 것을 볼 수 있기에 이분 그래프에 해당한다.
- 오른쪽 그림을 보면 5개의 변으로 구성된 그래프로써, 4개의 변은 색1(분홍)과 색2(초록)의 노드를 포함하는 것을 볼 수 있지만, 나머지 하나의 변이 색1(분홍)과 색1(분홍)의 노드를 포함하므로 이분 그래프가 아니다.
이러한 개념을 가지고 문제를 풀어보겠다.
소스코드 상에 주석으로 자세한 설명을 적어놓았지만, 다시한번 설명하겠다.
1. 우선 벡터(또는 배열)를 통해 그래프 정보를 입력받는다.
2. 그래프를 BFS 또는 DFS 알고리즘을 통해 탐색을 진행한다. (각각 코딩하여 진행하였음)
탐색중에 방문한 노드를 기존에는 true로 표현했지만, 해당 문제에서는 1(RED)와 2(BLUE) 그리고 0(방문x) 로 표현된다.
2-1. bfs
시작 노드의 색상을 RED로 지정하고(아무색상). 시작 노드와 링크로 연결된 노드들은 시작노드와 반대되는 색상(BLUE)으로 지정한다. 이 포인트를 기억하면서 코딩하면 쉽게 풀 수 있다.
2-2. dfs
초기 방문노드를 RED로 지정하고(아무색상). 지정노드와 재귀함수를 통해 링크로 연결된 노드들은 반대되는 색상(BLUE)으로 지정한다. 이 포인트를 기억하면서 코딩하면 쉽게 풀 수 있다.
3. 이분 그래프 여부를 체크 및 결과출력
4. (테스트 케이스가 1 이상이므로) 그래프 및 방문기록 초기화
| 소스 코드 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
|
#include <iostream>
#include <vector>
#include <queue> // use bfs algorithm
#include <stdio.h> // use printf, scanf
#include <cstring> // use memset
#define MAX_SIZE 20000+1
#define RED 1
#define BLUE 2
using namespace std;
int K, V, E; // 테스트 케이스, 노드, 링크 선언
vector<int> graph[MAX_SIZE];
int visited[MAX_SIZE];
void bfs(int start);
bool isBipartiteGraph();
void bfs(int start) {
queue<int> q;
int color = RED; // 시작 노드의 default 색상은 RED.
visited[start] = color;
q.push(start);
while (!q.empty()) {
int now = q.front();
q.pop();
if (visited[now] == RED) {
color = BLUE;
}
else if (visited[now] == BLUE) {
color = RED;
}
int gsize = graph[now].size();
for (int i = 0; i < gsize; i++) {
int next = graph[now][i];
if (!visited[next]) {
visited[next] = color;
q.push(next);
}
}
}
}
void dfs(int start) {
if (!visited[start]) {
visited[start] = RED;
}
int gsize = graph[start].size();
for (int i = 0; i < gsize; i++) {
int next = graph[start][i];
if (!visited[next]) {
if (visited[start] == RED) {
visited[next] = BLUE;
}
else if (visited[start] == BLUE) {
visited[next] = RED;
}
dfs(next);
}
}
}
bool isBipartiteGraph() {
for (int i = 1; i <= V; i++) {
int gsize = graph[i].size();
for (int j = 0; j < gsize; j++) {
int next = graph[i][j];
if (visited[i] == visited[next]) {
return 0;
}
}
}
return 1;
}
int main() {
scanf("%d", &K);
while (K--) {
scanf("%d %d", &V, &E);
/* 그래프 정보 입력 */
for (int i = 0; i < E; i++) {
int f, s;
scanf("%d %d", &f, &s);
graph[f].push_back(s);
graph[s].push_back(f);
}
/* 그래프를 BFS 또는 DFS를 통해 탐색 */
for (int i = 1; i <= V; i++) {
if (!visited[i]) { // 해당 노드를 아직 방문하지 않았다면,
bfs(i);
//dfs(i);
}
}
/* 이분 그래프 여부 체크 및 결과출력 */
if (isBipartiteGraph()) {
printf("YES\n");
}
else {
printf("NO\n");
}
/* 그래프 및 방문기록 초기화 */
for (int i = 0; i <= V; i++) {
graph[i].clear();
}
memset(visited, false, sizeof(visited));
}
return 0;
}
|
'백준 > BFS' 카테고리의 다른 글
| [백준 2178, c++] 미로탐색(bfs) (0) | 2019.11.12 |
|---|---|
| [백준 4963, c++] 섬의 개수(bfs,dfs) (0) | 2019.11.12 |
| [백준 11724, c++] 연결 요소의 개수(bfs, dfs) (0) | 2019.11.10 |
| [백준 1260, c++] DFS와 BFS (0) | 2019.10.07 |
| [백준 2667, c++] 단지번호붙이기 BFS(queue) (0) | 2019.10.07 |