| 문제 번호 |
| 문제 및 입/출력 |
요즘 민규네 동네에서는 스타트링크에서 만든 PS카드를 모으는 것이 유행이다.
PS카드는 PS(Problem Solving)분야에서 유명한 사람들의 아이디와 얼굴이 적혀있는 카드이다. 각각의 카드에는 등급을 나타내는 색이 칠해져 있고, 다음과 같이 8가지가 있다.
- 전설카드
- 레드카드
- 오렌지카드
- 퍼플카드
- 블루카드
- 청록카드
- 그린카드
- 그레이카드
카드는 카드팩의 형태로만 구매할 수 있고, 카드팩의 종류는 카드 1개가 포함된 카드팩, 카드 2개가 포함된 카드팩, ... 카드 N개가 포함된 카드팩과 같이 총 N가지가 존재한다.
민규는 카드의 개수가 적은 팩이더라도 가격이 비싸면 높은 등급의 카드가 많이 들어있을 것이라는 미신을 믿고 있다. 따라서, 민규는 돈을 최대한 많이 지불해서 카드 N개 구매하려고 한다. 카드가 i개 포함된 카드팩의 가격은 Pi원이다.
예를 들어, 카드팩이 총 4가지 종류가 있고, P1 = 1, P2 = 5, P3 = 6, P4 = 7인 경우에 민규가 카드 4개를 갖기 위해 지불해야 하는 금액의 최댓값은 10원이다. 2개 들어있는 카드팩을 2번 사면 된다.
P1 = 5, P2 = 2, P3 = 8, P4 = 10인 경우에는 카드가 1개 들어있는 카드팩을 4번 사면 20원이고, 이 경우가 민규가 지불해야 하는 금액의 최댓값이다.
마지막으로, P1 = 3, P2 = 5, P3 = 15, P4 = 16인 경우에는 3개 들어있는 카드팩과 1개 들어있는 카드팩을 구매해 18원을 지불하는 것이 최댓값이다.
카드 팩의 가격이 주어졌을 때, N개의 카드를 구매하기 위해 민규가 지불해야 하는 금액의 최댓값을 구하는 프로그램을 작성하시오. N개보다 많은 개수의 카드를 산 다음, 나머지 카드를 버려서 N개를 만드는 것은 불가능하다. 즉, 구매한 카드팩에 포함되어 있는 카드 개수의 합은 N과 같아야 한다.
입력
첫째 줄에 민규가 구매하려고 하는 카드의 개수 N이 주어진다. (1 ≤ N ≤ 1,000)
둘째 줄에는 Pi가 P1부터 PN까지 순서대로 주어진다. (1 ≤ Pi ≤ 10,000)
출력
첫째 줄에 민규가 카드 N개를 갖기 위해 지불해야 하는 금액의 최댓값을 출력한다.
| 예제 입력1 |
| 4 1 5 6 7 |
| 예제 출력1 |
| 10 |
| 예제 입력2 |
| 5 10 9 8 7 6 |
| 예제 출력2 |
| 50 |
| 예제 입력3 |
| 10 1 1 2 3 5 8 13 21 34 55 |
| 예제 출력3 |
| 55 |
| 예제 입력4 |
| 10 5 10 11 12 13 30 35 40 45 47 |
| 예제 출력4 |
| 50 |
| 예제 입력5 |
| 4 5 2 8 10 |
| 예제 출력5 |
| 20 |
| 예제 입력6 |
| 4 3 5 15 16 |
| 예제 출력1 |
| 18 |
| 문제 풀이 |
Dynamic Programming(DP)를 통해 풀 수 있는 문제이다.
- 최대한 돈을 많이 지불해서 카드 N개를 구매하려한다.
- 카드 i개가 포함된 카드팩의 가격은 Pi원이다.
- 입력으로 구매하려하는 카드의 갯수 n개와 카드팩의 가격 Pi는 주어진다.
문제가 조금 길지만 중요한 포인트만 꼽자면 위에 세 줄이 될거같다. 결국 카드 팩의 가격이 주어졌을 때, N개의 카드를 구매하기 위해 민규가 지불해야 하는 금액의 최댓값을 구하는 프로그램을 작성하는 것이다.
나는 예제 2번을 선택해서 점화식을 구하기위해 규칙을 찾아보았다.
예제 2번은 n = 5이고, P1 = 10, P2 = 9, P3 = 8, P4 = 7, P5 = 6이 된다.
n = 1개의 카드를 구매하려 할 때, 카드 1개가 포함된 P1을 구매하는 한 가지 방법이 존재한다. 여기서 MAX_COST1 = P1 = 10이 된다.
n = 2개의 카드를 구매하려 할 때, 카드 2개가 포함된 P2를 구매하거나, MAX_COST1 + P1을 구매하는 두 가지 방법이 존재하는데 둘 중에 COST가 높은 것을 MAX_COST로 설정한다. 여기서 MAX_COST2 = 20이 된다.
n = 3개의 카드를 구매하려 할 때, 카드 3개가 포함된 P3를 구매하거나, MAX_COST2 + P1, MAX_COST1 + P2의 세 가지 방법이 존재하는데, 셋 중에 COST가 높은 것을 MAX_COST로 설정한다. 여기서 MAX_COST3 = 30 이 된다.
......
결과적으로 MAX_COST5 = 50이 된다.
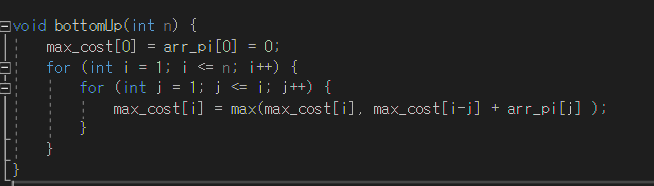
결과적으로 위 사진처럼 이중포문으로 구성이 되고, 점화식은 MAX_COST(i)= MAX(MAX_COST(i) , MAX_COST(i-j) + P(j))가 된다.
| 소스 코드 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
#define MAX 1000
int arr_pi[MAX + 1];
int max_cost[MAX + 1];
int max(int a, int b) {
if (a > b) return a; return b;
}
void bottomUp(int n) {
max_cost[0] = arr_pi[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
max_cost[i] = max(max_cost[i], max_cost[i-j] + arr_pi[j] );
}
}
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &arr_pi[i]);
}
bottomUp(n);
printf("%d\n", max_cost[n]);
return 0;
}
|
'백준 > DP' 카테고리의 다른 글
| [백준 15990, c++] 1,2,3 더하기 5(dp:bottomUp) (2) | 2019.12.08 |
|---|---|
| [백준 16194, c++] 카드 구매하기 2(dp: bottomUp) (0) | 2019.12.05 |
| [백준 15988, c++] 1,2,3 더하기 3(dp: topDown, bottomUp) (0) | 2019.11.28 |
| [백준 9095, c++] 1,2,3 더하기(dp: topDown, bottomUp) (0) | 2019.11.27 |
| [백준 11727, c++] 2xn 타일링2(dp,topDown,bottomUp) (0) | 2019.11.26 |