| 스택이란? |
스택(stack)은 컴퓨터에서 믿을 수 없을 정도로 많이 사용되는 자료구조이다. 창고에 쌓여있는 상자나 책 등을 생각하면 스택을 이해하기가 더 쉽다. 아래서 부터 A,B,C,D 순으로 쌓여있는 상자에서 B의 상자를 꺼내고 싶다면 D -> C -> B 순으로 상자를 건드리면서 꺼내야한다.
Ex> 스마트폰에서 '뒤로가기' 키를 누르면 현재 수행되는 앱이 종료되고, 이전에 수행되던 앱이 다시 나타난다.
Ex> 컴퓨터 안에서는 수 많은 함수 호출이 이루어지고, 이러한 함수는 실행이 끝나면 자신을 호출한 장소로 되돌아가야한다. 이때 스택이 사용된다. 즉, 스택은 복귀할 주소를 기억하는데 사용된다.
Ex> 컴파일러안에 괄호 사용의 오류를 검사하는데에도 쓰인다. 괄호는 대괄호[], 중괄호{}, 소괄호() 등이 있는데, 코드 상에서 이 괄호의 구조는 "가장 가까운 거리에 있는 괄호들끼리 서로 쌍을 이루는 특징"을 갖고 있기 때문에 스택을 사용하여 왼쪽 괄호들을 만나면 계속 삽입하다가 오른쪽 괄호들이 나올 때 스택에서 가장 최근의 왼쪽 괄호를 꺼내어 타입을 비교하여 쉽게 괄호 오류를 검출해 낼 수 있다.
Ex> 컴파일러안에 수식을 계산할 때도 스택이 쓰인다. 우리는 중위(infix) 표기법을 통해 수식을 작성한다. 하지만 대부분의 컴파일러는 이것을 후위(postfix) 표기법으로 변환한 후에 스택을 이용하여 계산한다. 후위 표기법을 쓰면 1. 괄호가 필요 없다 2. 연산자의 우선순위도 생각할 필요가 없다 3. 수식을 읽으면서 바로 계산 한다라는 세 가지 중요한 장점을 갖고 있다. 수식을 왼쪽에서 오른쪽으로 스캔하여 피연산자이면 스택에 저장하고 연산자이면 필요한 수만큼의 피연산자를 스택에서 꺼내 연산을 실행하고 연산의 결과를 다시 스택에 저장하는 방식으로 수행된다.
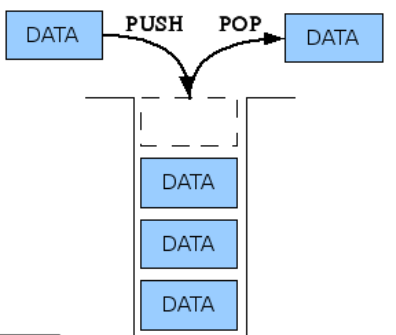
- 후입선출(LIFO: Last-In First-Out) : 가장 최근에 들어온 데이터가 가장 위에 위치하게 되고, 가장 먼저 나가게 된다.
- 스택의 입출력은 맨 위에서만 일어나고 스택의 중간에서는 데이터를 삭제할 수 없다.
- 후입선출의 특징으로 자료의 출력순서가 입력순서의 역순으로 이루어져야 할 경우에 매우 긴요하게 사용된다.
- 스택을 구현하는 방법에는 1. 배열을 이용한 방법 2. 연결 리스트를 이용하는 방법이 있다. 배열을 이용한 방법은 구현이 간단하고 성능이 우수한 반면에 스택의 크기가 고정되는 단점이 있다. 연결 리스트를 이용하는 방법은 구현이 약간 복잡한 반면에 스택의 크기를 필요에 따라 가변적으로 구성할 수 있는 장점이 있다. (배열, 연결리스트)
| 동적 배열을 사용한 스택 |
동적 배열을 사용하여 구현한 stack 코드 분석을 통해 더 쉽게 이해해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
#include < stdio.h >
#include < stdlib.h >
#define MAX_STACK_SIZE 100
typedef int element;
typedef struct {
element *data; // data은 포인터로 정의된다.
int capacity; // 현재 크기
int top;
} StackType;
// 스택 생성 함수
void init_stack(StackType *s)
{
s->top = -1;
s->capacity = 1;
s->data = (element *)malloc(s->capacity * sizeof(element));
}
// 공백 상태 검출 함수
int is_empty(StackType *s)
{
return (s->top == -1);
}
// 포화 상태 검출 함수
int is_full(StackType *s)
{
return (s->top == (MAX_STACK_SIZE - 1));
}
void push(StackType *s, element item)
{
if (is_full(s)) {
s->capacity *= 2;
s->data =
(element *)realloc(s->data, s->capacity * sizeof(element));
}
s->data[++(s->top)] = item;
}
// 삭제함수
element pop(StackType *s)
{
if (is_empty(s)) {
fprintf(stderr, "스택 공백 에러\n");
exit(1);
}
else return s->data[(s->top)--];
}
int main(void)
{
StackType s;
init_stack(&s);
push(&s, 1);
push(&s, 2);
push(&s, 3);
printf("%d \n", pop(&s));
printf("%d \n", pop(&s));
printf("%d \n", pop(&s));
free(s.data);
return 0;
}
|
3
2
1
| 추천 문제 |
'백준 > 알고리즘 이론정리' 카테고리의 다른 글
| [알고리즘 이론] 연결 리스트(Linked List) (0) | 2020.04.17 |
|---|---|
| [알고리즘 이론] 큐(Queue) (0) | 2020.04.15 |
| [필수알고리즘, python] 연결 리스트(Linked list) (0) | 2019.11.07 |