| 문제 번호 |
| 문제 및 입/출력 |
45656이란 수를 보자.
이 수는 인접한 모든 자리수의 차이가 1이 난다. 이런 수를 계단 수라고 한다.
세준이는 수의 길이가 N인 계단 수가 몇 개 있는지 궁금해졌다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구하는 프로그램을 작성하시오. (0으로 시작하는 수는 없다.)
입력
첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
| 예제 입력1 |
| 1 |
| 예제 출력1 |
| 9 |
| 예제 입력2 |
| 2 |
| 예제 출력2 |
| 17 |
| 문제 풀이 |
dynamic programming(dp)를 통해 간단하게 풀 수 있는 문제이다.
# 점화식 구하기
- 인접한 모든 자리수의 차이가 1이나는 계단 수를 갖는다.
- 즉, 어떤 수(num)가 있으면 인접한 수는 어떤 수(num)의 -1 또는 +1이 된다.
- 0으로 시작하는 수는 없다. (0으로 끝나는건 가능)
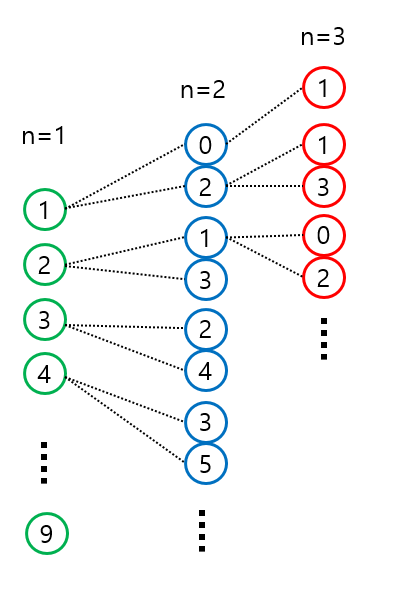
쉬운 이해를 돕기위해 길이 n에 따라 어떤 결과들이 나열되는지 그림으로 표현해보았다.
우선 n=1일때는 1~9까지의 초록색 리스트를 띄고있다.
그리고 n=2일때는 1부터 나열하면 10,12,21,23 순서로 나열되는데 여기서 바로 규칙을 찾을 수 있다. 바로 초록색 리스트에서 각각 숫자마다 +1,-1의 리스트가 n = 2일때의 총 계단 수(파란색 리스트)가 된다는 것이다.
또 n=3일때는 파란색 리스트를 기준으로 -1,+1의 리스트를 구하면 위 빨간색 리스트와 같은 총 계단의 수가 구해진다.
이를 통해 쉽게 점화식을 구할 수 있는데,
dp[length][num]가 n의 길이가 length일때, num이 0~9일 경우의 수 라고 이중 배열을 구성했을때,
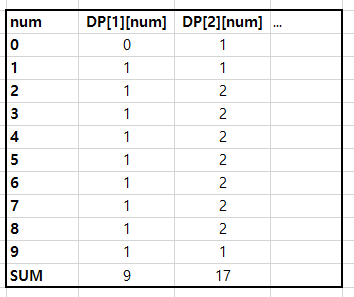
dp[1][num] 일때는 한 자리 수 이므로 1~9까지 각각 하나의 경우의 수가 존재하고,
dp[2][num] 일때는 두 자리 수이므로 위 그림1처럼 규칙에 따라 나뉘어져서 각각의 num의 경우의 수가 계산된다.
...
결과적으로 아래와 같이 점화식을 구할 수 있다.
dp[length][num] = dp[length-1][num-1] + dp[length-1][num+1]
| 소스 코드 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#include <iostream>
#include <cstdio>
using namespace std;
const int mod = 1e9;
const int MAXN = 100;
int dp[MAXN + 1][10];
int bottomUp(int n) {
for (int i = 1; i < 10; i++)
dp[1][i] = 1;
for (int length = 2; length <= n; length++) {
for (int num = 0; num < 10; num++) {
if (num == 0) {
dp[length][num] = dp[length - 1][num + 1] % mod;
}
else if (num == 9) {
dp[length][num] = dp[length - 1][num - 1] % mod;
}
else {
dp[length][num] = (dp[length - 1][num - 1] + dp[length - 1][num + 1]) % mod;
}
}
}
int sum = 0;
for (int i = 0; i < 10; i++)
sum = (sum + dp[n][i]) % mod;
return sum;
}
int main() {
int n;
scanf("%d", &n);
printf("%d\n", bottomUp(n));
return 0;
}
|
'백준 > DP' 카테고리의 다른 글
| [백준 2193, c++] 이친수(dp:bottomUp) (0) | 2019.12.13 |
|---|---|
| [백준 11057, c++] 오르막 수(dp: bottomUp) (0) | 2019.12.11 |
| [백준 15990, c++] 1,2,3 더하기 5(dp:bottomUp) (2) | 2019.12.08 |
| [백준 16194, c++] 카드 구매하기 2(dp: bottomUp) (0) | 2019.12.05 |
| [백준 11052, c++] 카드 구매하기(dp: bottomUp) (0) | 2019.11.28 |