| 문제 번호 |
| 문제 및 입/출력 |
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.
예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.
수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.
입력
첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.
출력
첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.
| 예제 입력1 |
| 1 |
| 예제 출력1 |
| 10 |
| 예제 입력2 |
| 2 |
| 예제 출력2 |
| 55 |
| 예제 입력3 |
| 3 |
| 예제 출력3 |
| 220 |
| 문제 풀이 |
dynamic programming(dp)를 통해 간단하게 풀 수 있는 문제이다.
# 점화식 구하기
- 수의 자리가 오름차순을 이룬다. (인접한 수가 같아도 오름차 순으로 친다)
- 즉 i번째 숫자가 i-1번째 숫자보다 크거나 같으면 오름차순으로 친다.
- 수는 0으로 시작할 수 있다.
다음과 같은 규칙을 가지고 길이 n에 따른 숫자들을 나열하면 아래 그림1과 같다.
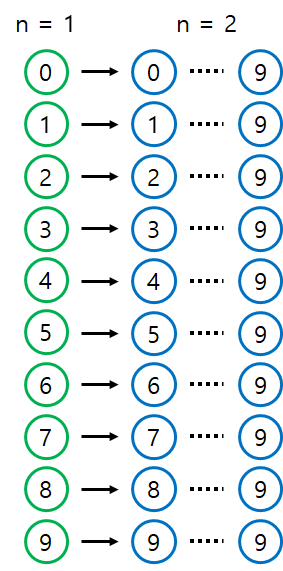
n = 1 일때, 한 자리수이므로 0~9까지 총 10개의 숫자가 존재한다.
n = 2 일때, 두 자리수이므로 (00, 01, 02, ... ,09), (11, 12, 13, .., 19), ...,(88, 89), (99)로 총 55개의 숫자가 존재한다.
여기까지만 보아도 규칙을 찾을 수 있다.
그림 1과 같이 n = 2번째의 구조를 보면 n = 1의 각각의 숫자들을 십의 자리로 구성하고, 해당 숫자에서 최대 숫자인 9까지를 일의 자리로 구성되있는 규칙을 찾을 수 있다.
결과적으로 점화식은(n = 1일때의 결과 값은 계산전에 미리 메모이제이션 해둔다)
for(s=2;s<n;s++)
for(i=0;i<10;i++)
for(j=i;j<10;j++)
dp[s][i] += dp[s - 1][j]
여기서 dp[s][i] 는 수의 길이가 s일때, 일의자리가 숫자 i가 될 경우의 숫자를 나타낸다.
| 소스 코드 |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include <iostream>
#include <cstdio>
using namespace std;
const int mod = 1e4+7;
const int MAXN = 1000;
int dp[MAXN + 1][10];
int bottomUp(int n) {
for (int i = 0; i < 10; i++)
dp[1][i] = 1;
for (int s = 2; s <= n; s++) {
for (int i = 0; i < 10; i++) {
for (int j = i; j < 10; j++) {
dp[s][i] += dp[s - 1][j] % mod;
}
}
}
int sum = 0;
for (int i = 0; i < 10; i++)
sum = (sum + dp[n][i]) % mod;
return sum;
}
int main() {
int n;
scanf("%d", &n);
printf("%d\n", bottomUp(n));
return 0;
}
|
'백준 > DP' 카테고리의 다른 글
| [백준 9465, c++] 스티커(dp:bottomUp) (0) | 2019.12.23 |
|---|---|
| [백준 2193, c++] 이친수(dp:bottomUp) (0) | 2019.12.13 |
| [백준 10844, c++] 쉬운 계단 수(dp: bottomUp) (0) | 2019.12.10 |
| [백준 15990, c++] 1,2,3 더하기 5(dp:bottomUp) (2) | 2019.12.08 |
| [백준 16194, c++] 카드 구매하기 2(dp: bottomUp) (0) | 2019.12.05 |